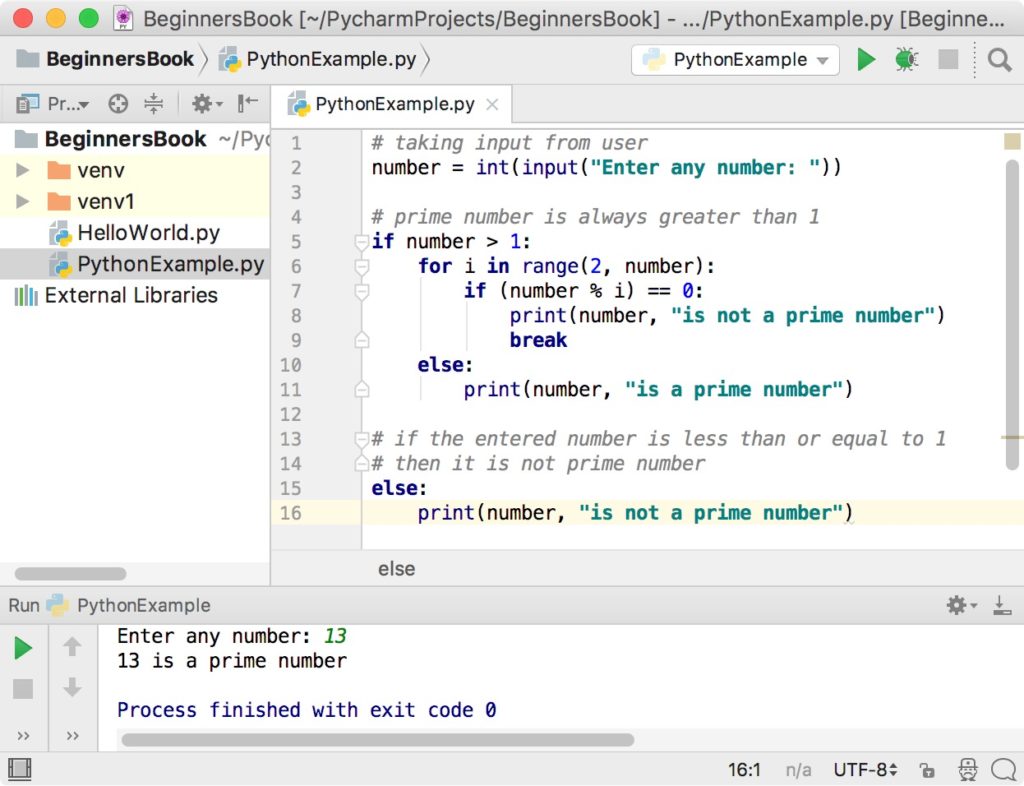
Prime Number Using Sqrt
Primes in the arithmetic progressions modulo 9. Each row of the thin horizontal band shows one of the nine possible progressions mod 9, with prime numbers marked in red.
The progressions of numbers that are 0, 3, or 6 mod 9 contain at most one prime number (the number 3); the remaining progressions of numbers that are 2, 4, 5, 7, and 8 mod 9 have infinitely many prime numbers, with similar numbers of primes in each progressionThe shows that there are arbitrarily long finite arithmetic progressions consisting only of primes. Prime values of quadratic polynomials. The small gear in this piece of farm equipment has 13 teeth, a prime number, and the middle gear has 21, relatively prime to 13For a long time, number theory in general, and the study of prime numbers in particular, was seen as the canonical example of pure mathematics, with no applications outside of mathematics other than the use of prime numbered gear teeth to distribute wear evenly. In particular, number theorists such as mathematician prided themselves on doing work that had absolutely no military significance.This vision of the purity of number theory was shattered in the 1970s, when it was publicly announced that prime numbers could be used as the basis for the creation of algorithms.These applications have led to significant study of for computing with prime numbers, and in particular of, methods for determining whether a given number is prime.The most basic primality testing routine, trial division, is too slow to be useful for large numbers. One group of modern primality tests is applicable to arbitrary numbers, while more efficient tests are available for numbers of special types.
Most primality tests only tell whether their argument is prime or not. Routines that also provide a prime factor of composite arguments (or all of its prime factors) are called algorithms.Prime numbers are also used in computing for, and.Trial division. The connected sum of two prime knotsThe concept of prime number is so important that it has been generalized in different ways in various branches of mathematics. Generally, 'prime' indicates minimality or indecomposability, in an appropriate sense. For example, the of a given field is its smallest subfield that contains both 0 and 1.
It is either the field of rational numbers or a with a prime number of elements, whence the name. Often a second, additional meaning is intended by using the word prime, namely that any object can be, essentially uniquely, decomposed into its prime components. For example, in, a is a that is indecomposable in the sense that it cannot be written as the of two nontrivial knots. Any knot can be uniquely expressed as a connected sum of prime knots. The is another example of this type.Beyond mathematics and computing, prime numbers have potential connections to, and have been used metaphorically in the arts and literature. They have also been used in to explain the life cycles of.Constructible polygons and polygon partitions.
Prime Number Using Sqrt Formula
Prime numberat Wikipedia's. from Wiktionary.
from Wikimedia Commons. from Wikinews. from Wikiquote. from Wikisource. from Wikibooks. from Wikiversity., ed.
(2001) 1994, Springer Science+Business Media B.V. / Kluwer Academic Publishers,. Caldwell, Chris, The at. on at the. from Plus, the free online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge.Generators and calculators. identifies the smallest prime factor of a number.
Prime Number Using Sqrt 8

makes use of the Elliptic Curve Method (up to thousand-digits numbers, requires Java).
